1.5. Dinámica de los sistemas ambientales
Las variables de estado, los flujos y los ciclos de retroalimentación son claves en el diseño de un modelo y van a determinar el comportamiento dinámico del sistema que representan. Cuando hablamos de dinámica de un sistema nos referimos a la variación temporal de las variables de estado cuyos valores pueden crecer, decaer u oscilar a lo largo del tiempo. Un sistema ambiental puede mostrar diferentes patrones de variación temporal, de los cuales hemos seleccionado los seis más importantes:
|
- El crecimiento exponencial es la dinámica más importante que podemos encontrar en un sistema ambiental. El crecimiento exponencial puede ser sorprendente rápido pues el sistema duplica su tamaño una y otra vez, en el mismo intervalo de tiempo. Este intervalo es conocido como el tiempo de duplicación. Ejemplo: Crecimiento de una población sin factores limitantes con una tasa de natalidad mayor que la tasa de mortalidad.
- El decaimiento exponencial es el inverso del crecimiento exponencial. El sistema perderá la mitad de su valor en un intervalo fijo de tiempo y así sucesivamente. Ejemplo: Crecimiento de una población sin factores limitantes con una tasa de natalidad menor que la tasa de mortalidad.
- La aproximación exponencial se parece a la decadencia exponencial, pero en este caso el sistema no decae hasta alcanzar el valor cero. Esto puede ocurrir cuando el sistema recibe un flujo de entrada que contrarresta el efecto de la decadencia. Estos sistemas pueden alcanzar el equilibrio gradualmente. Ejemplo: Crecimiento de una población sin factores limitantes con una tasa de natalidad menor que la tasa de mortalidad pero con reclutamiento de nuevos individuos por migración.
|
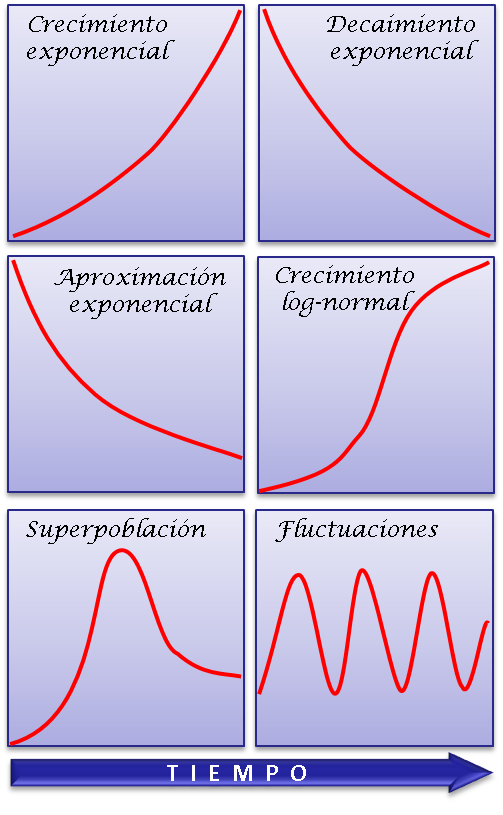 |
- El crecimiento
log-normal se parece al patrón de crecimiento exponencial en las etapas
tempranas. Pero cuando el sistema avanza en el tiempo y crece cada vez
más, llega un momento en que no puede seguir creciendo por que alcanza
un límite final. Los límites vienen impuestos por las restricciones
sobre los recursos o los nutrientes disponibles en el hábitat. Para que
una variable de estado muestre un patrón de crecimiento log-normal, el
sistema debe sentir el efecto limitante de manera que disminuya la
velocidad de crecimiento gradualmente y permita al sistema llegar a un
estado de equilibrio que puede ser mantenido año tras año. Ejemplo:
Crecimiento de una población con un limite impuesto por su capacidad de
carga.
- El patrón de
superpoblación (Overshoot) se inicia de la misma manera que el
crecimiento log-normal, pero en este caso el sistema no consigue
adaptarse progresivamente a sus recursos limitados. Si hay demoras en la
reacción a los límites, el crecimiento tiende a llevar al sistema más
allá de valores sostenibles que posteriormente dará lugar a una caída
brusca hasta alcanzar de nuevo valores sostenibles. Este tipo de
dinámicas son propias de sistemas humanos como los sistemas económicos.
- Las fluctuaciones son
patrones muy comunes en muchos sistemas, se trata de oscilaciones
repetitivas y estables en el tiempo que aseguran la longevidad del
sistema. En muchos sistemas las fluctuaciones surgen como resultado de
simples demoras en el crecimiento de los componentes del sistema, como
es el caso del modelo predador-presa.
|
Obra colocada bajo licencia Creative Commons Attribution-NonCommercial-NoDerivs 2.5 License
