2. Física de la radiación

LEY DE PLANCK

No todas las superficies emiten o absorben la misma cantidad de energía radiante cuando se calientan a la misma temperatura. Un cuerpo que absorba o emita a una temperatura determinada la máxima cantidad de energía posible se denomina superficie negra o simplemente cuerpo negro. n cuerpo negro perfecto no existe en la realidad, sino que es un ente ideal que se utiliza como referencia respecto a otros cuerpos radiantes. No obstante, existen numerosas superficies que son cuerpos negros casi perfectos, sobre todo para radiaciones de onda larga, por lo que para casos prácticos son considerados como tales con suficiente exactitud.

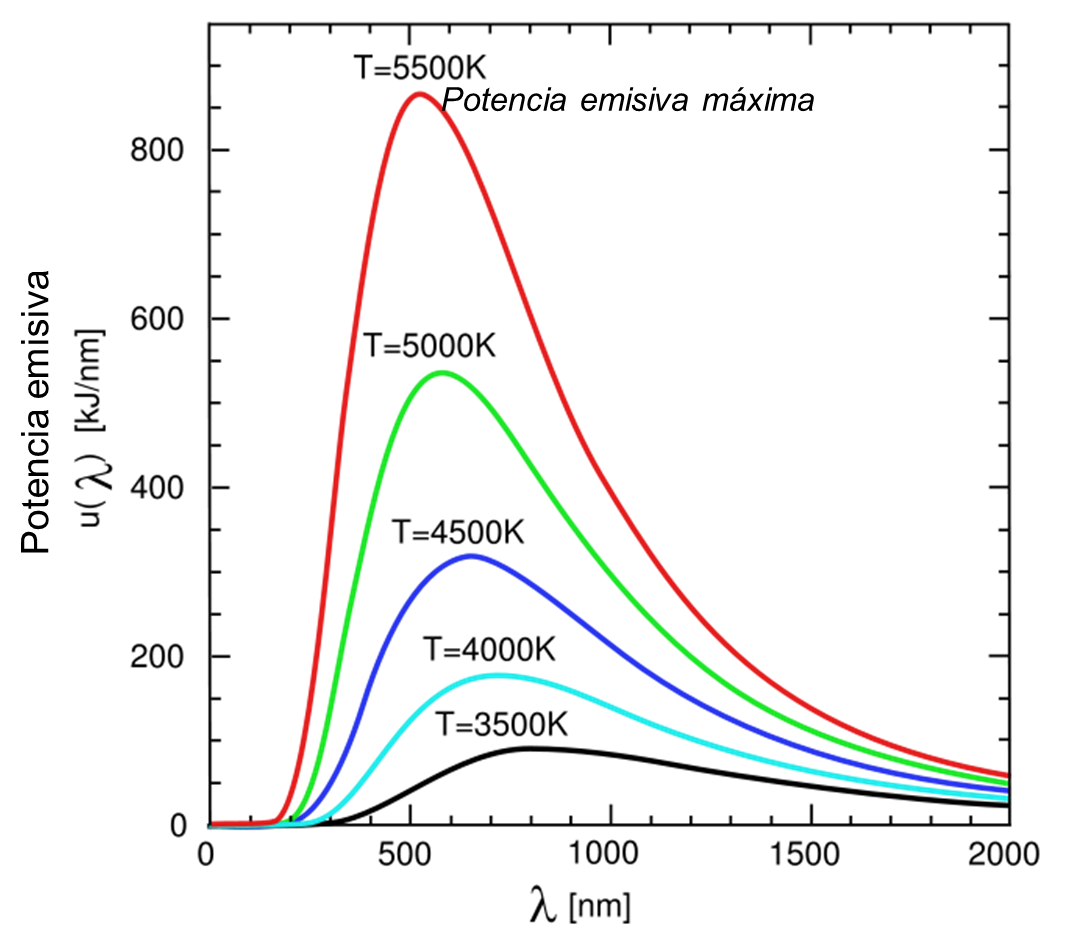
Cuando un cuerpo negro se calienta a una temperatura absoluta, T, su superficie emite un flujo de radiación térmica con una distribución espectral definida, que es determinable mediante la Ley de Planck:

Siendo:

Q_0λ:Poder emisivo espectral en función de la longitud de onda [W/m²]
λ:  Longitud de onda [m]
T:  Temperatura absoluta [ºK]
C₁: 1ª Cte. radiación = 3.7418·10^-16 [W m²]
C₂: 2ª Cte. radiación = 1.4388·10^-2 [m ºK]

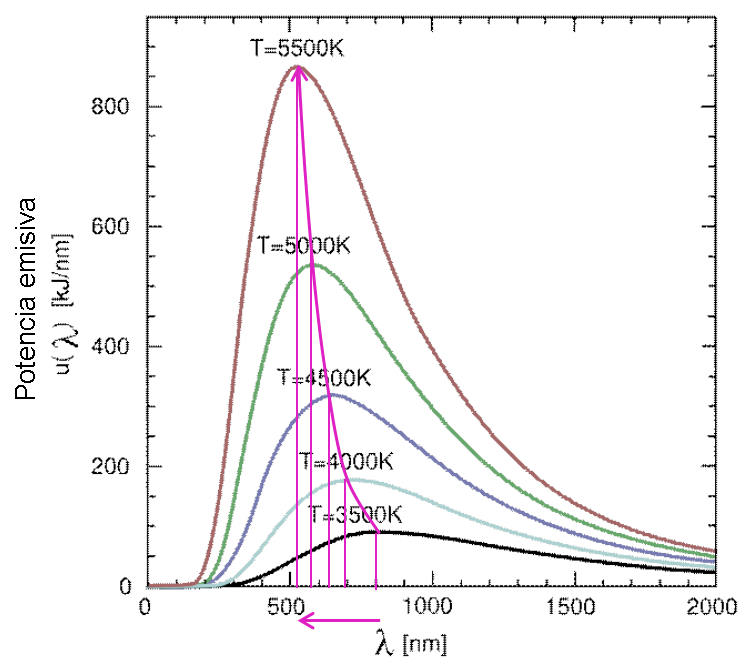
LEY DEL DESPLAZAMIENTO DE WIEN

La longitud de onda a la cual la potencia emisiva es máxima se puede deducir de la Ley de Planck, derivándola respecto a λ, igualando a 0 y despejando λ.

[m]

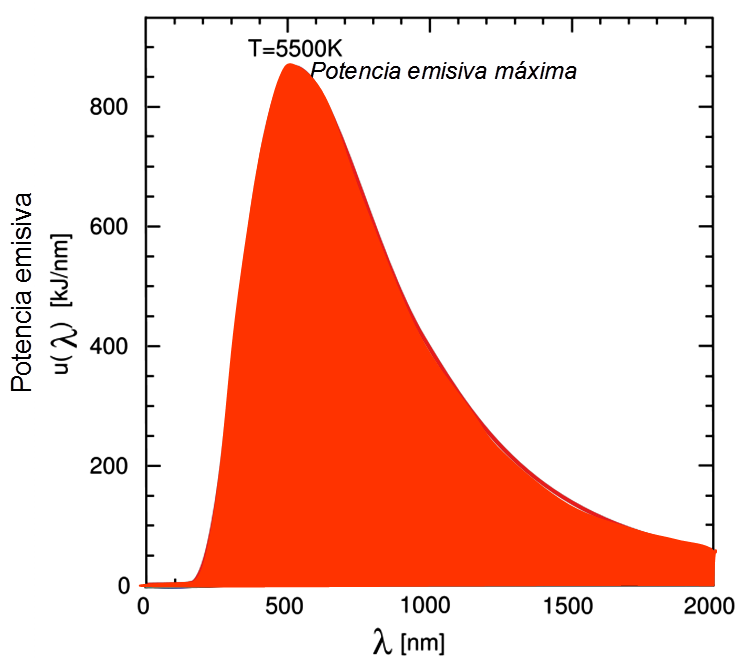
LEY DE STEFAN-BOLTZMANN

El flujo total de energía radiante que emite un cuerpo negro en todo el espectro a una temperatura absoluta T se determina integrando la distribución de Planck para todas las longitudes de onda, cuyo resultado se conoce como la Ley de Stefan-Boltzmann:

[W/m²]

siendo σ = 5.67·10-8 [W/m² ºK⁴] la Constante de Stefan-Boltzmann.